旅游怎么做攻略
查询气候与季节:根据目的地气候特点准备衣物。如东南亚雨季需携带防水装备,北欧冬季需准备防寒衣物。同时,结合季节规划活动(如春季赏樱、冬季滑雪)。 参考权威攻略与避坑指南利用旅游平台:携程、马蜂窝:查看景点评分、游客实拍图及详细攻略,重点关注“最新提示”板块(如临时闭馆、门票优惠)。
做旅游攻略可按以下四个步骤进行:明确核心框架:先确定目的地与兴趣,依据季节和个人偏好来挑选,比如夏季避暑可去青岛、长白山,想体验文化可选西安、南京。接着锁定时间与预算,明确旅行天数和人均预算,预算有限就优先选择周边或交通便利的目的地。
做旅游攻略可按以下详细步骤进行:明确核心要素:确定目的地,综合预算、时间、兴趣来选择,比如喜欢自然风光可去黄山;设定基础框架,明确出行时间、同行人员和预算分配,家庭游要考虑儿童设施,交通、住宿、餐饮预算占比建议为5:3:2。
出去旅游做攻略的方法主要包括以下几点: 选定游玩地点 明确目的地:根据个人爱好选择游玩地点,可以是著名的景点,也可以是悠闲的小镇。确定一个或多个目的地,并在地图上进行标注或记录下来,以便后续安排路线。规划游玩内容:了解目的地的特色景点、文化活动等,根据自己的兴趣和时间制定游玩计划。
学会做旅游攻略需要从前期准备、信息收集、行程规划、核实资讯到当地注意事项等多个方面入手,以下是具体方法:前期准备必带物品:证件:身份证、学生证(如有)、车票、现金、信用卡。用品:手机(确保话费充足)、相机、充电器、遮阳伞、湿巾、卷纸面巾纸。
旅游攻略的制作需要系统性思维和个性化设计,我将从八个维度为你解析完整攻略制作流程:目的地筛选体系 地理特征分析:通过地形图、气候带分布了解最佳旅行季节。如东南亚11-2月为旱季,阿尔卑斯山区7-8月适合徒步。文化坐标定位:标记世界遗产、博物馆等核心文化节点。
我们身边的拓扑学:数学理论如何融入日常生活?
1、除了以上几个方面,拓扑学在日常生活中还有许多其他的应用。例如,在日常生活中,我们经常会遇到一些需要解开绳结的问题。通过对绳结的拓扑结构进行研究,我们可以找到一种更加简单、快捷的解结方法。这不仅提高了我们的生活质量,还让我们在解决日常问题时更加得心应手。在食品加工中,拓扑学的原理也可以应用于食品的包装和储存。
2、拓扑学是数学的一个分支,主要研究空间的性质和结构。尽管它看起来可能与我们的日常生活没有直接关系,但实际上,拓扑学在现代科学中有许多实际应用。首先,拓扑学在物理学中有广泛的应用。例如,量子场论中的路径积分就是基于拓扑学的。
3、拓扑学对连续性数学是带有根本意义的,对于离散性数学也起着巨大的推动作用。拓扑学的基本内容已经成为现代数学的常识。拓扑学的概念和方法在物理学、生物学、化学等学科中都有直接、广泛的应用。
4、机械性能在固体中的拓扑依赖性在机械工程和材料科学学科中。电气和机械性能取决于材料中分子和基本单元的布置和网络结构。研究了皱褶拓扑的抗压强度,试图了解这种主要是空白空间的结构的高强度重量。拓扑在接触力学中具有重要意义,其中刚度和摩擦对表面结构的维数的依赖性是多体物理学中应用的关注点。
数学与应用数学专业的研究热点
数学与应用数学专业的研究热点涵盖基础数学、计算数学、概率论与数理统计、应用数学、运筹学与控制论及跨学科方向六大领域。基础数学是数学学科的核心,聚焦代数、几何、拓扑等理论方向的研究。其成果不仅深化了数学自身的理论体系,更为物理学、计算机科学等其他学科提供了底层逻辑支持。
数学与应用数学(本科)+软件工程(研究生):同样适用于教育、公务员、人工智能、金融、软件等行业。数学与应用数学(本科)+金融学(研究生):适合准备在人工智能、金融、大数据等领域的学生。
基础数学 基础数学是数学科学的核心,也是其他应用性数学分支的基础,如微分几何、数学物理、偏微分方程等。它是研究事物的数量关系和空间形式的学科,不需要与其他学科的实际问题有直接联系。基础数学是数学专业考研方向之一,也是数学与应用数学专业考研方向之一。
数学与应用数学考研最佳方向:运筹学、计算数学、应用数学、金融方向。运筹学专业。运筹学用于解决现实生活中的复杂问题,特别是改善或优化现有系统的效率。研究运筹学的基础知识包括实分析、矩阵论、随机过程、离散数学和算法基础等。而在应用方面,多与仓储、物流、算法等领域相关。
sy1133(2004级应用数学博士):应用数学是交叉学科,所以我觉得只要有应用背景的数学问题都可以看作是这个学科的发展,从这个角度看,应用数学的发展是非常繁盛的。林彬彬(2007级应用数学硕士研究生):应用数学在国内起步比较晚,但很热门,不过国内发展水平和国际还有一定差距。
拓扑是什么东西
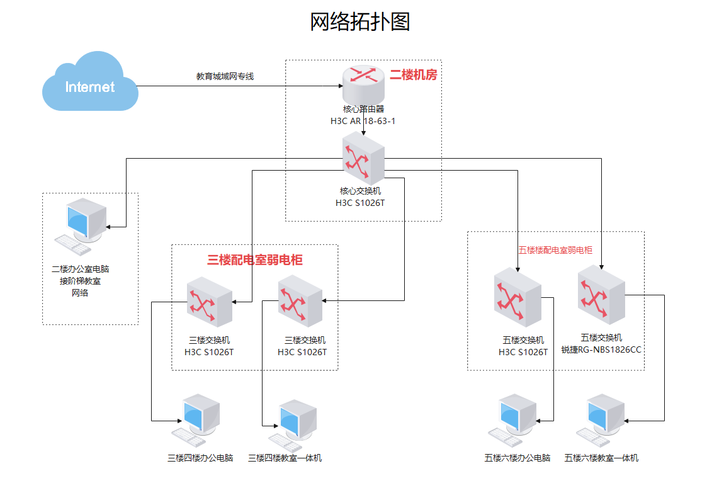
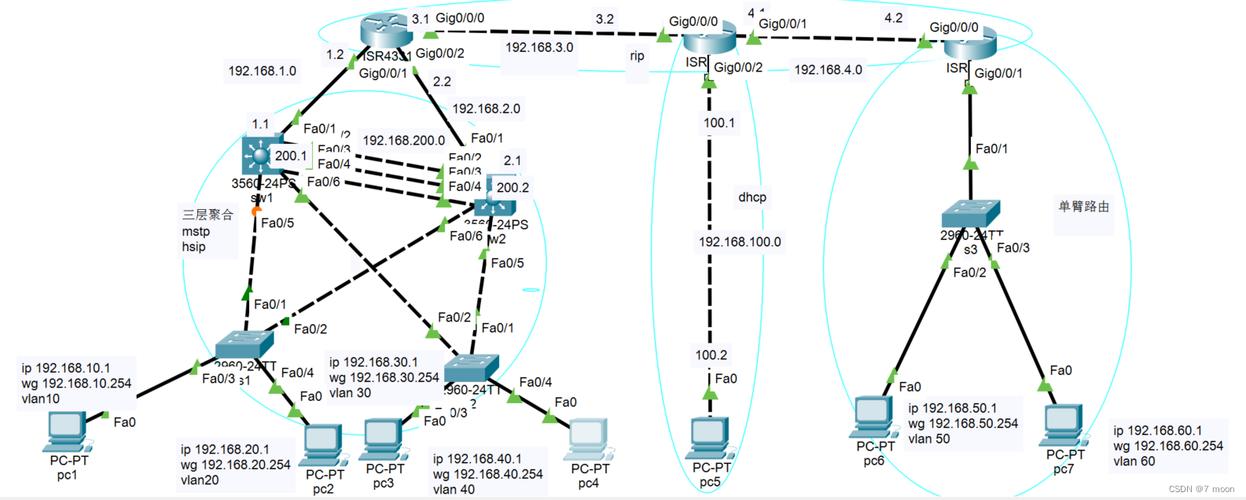
拓扑是一种几何结构,它描述的是网络中各个站点如何相互连接。常见的拓扑类型包括总线型、星型、环形和混合型。拓扑学则是一种以空间几何方式表现事物内部结构、原理和工作状态的方法。
拓扑,简单来说,就是研究物体在连续变形下还能保持不变的那些性质。就像你玩橡皮泥,不管你怎么捏、怎么拉伸,只要不断开,它都还是那块橡皮泥,这个“不断开”的性质,就是拓扑性质。
简单的说,拓扑实际上就是一个在空间和时间上的顺序关系,比如你上大学学习课程,在学专业课之前要学习相关的数学课,那么在拓扑关系上反映出来,数学就在专业课之前,这就是一个简单的拓扑关系,拓扑关系一般可以通过拓扑图显示出来。
本文来自作者[bjklfd]投稿,不代表康立号立场,如若转载,请注明出处:https://www.bjklfd.cn/zsbk/202511-13756.html



评论列表(3条)
我是康立号的签约作者“bjklfd”
本文概览:旅游怎么做攻略 查询气候与季节:根据目的地气候特点准备衣物。如东南亚雨季需携带防水装备,北欧冬季需准备防寒衣物。同时,结合季节规划活动(如春季赏樱、冬季滑雪)。 参考权威攻略与...
文章不错《拓扑学视角下的交通网络(拓扑学问题)》内容很有帮助